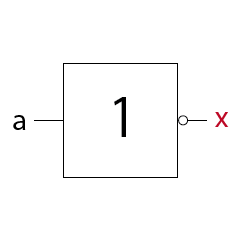
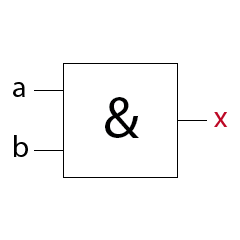
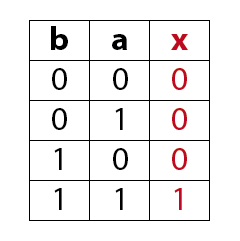
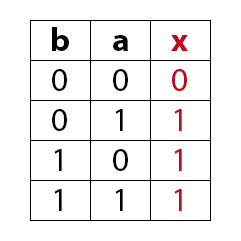
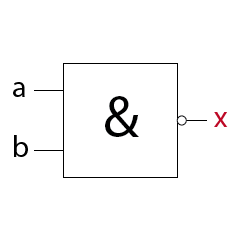
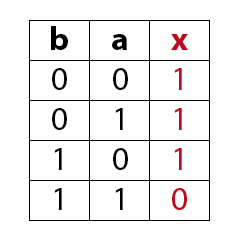
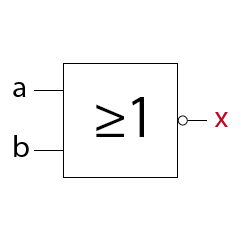
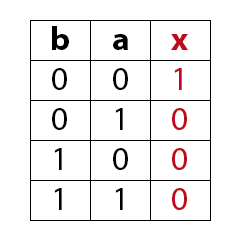
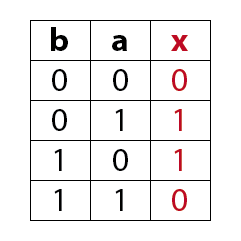
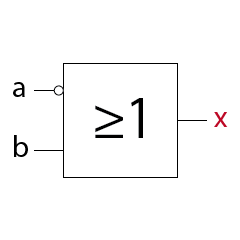
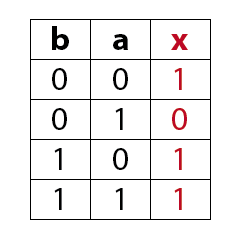
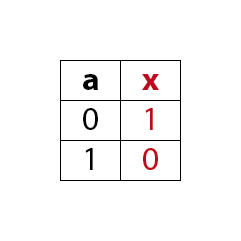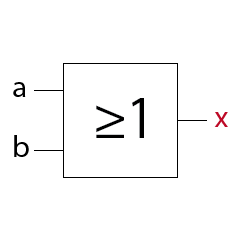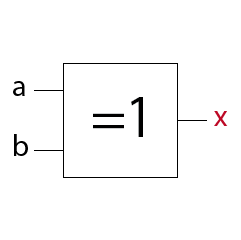MagicNumbers ist ein Kartenspiel mit dem du durchaus einige Menschen beeindrucken kannst. Es basiert auf der binären Darstellung der Zahlen 1 bis 31. Für die Darstellung der Zahlen (0)1-31 benötigst du im dualen oder binären Zahlensystem 5 Bits (25 = 32). Die Anzahl der Bits ist gleich der Anzahl der daraus resultierenden Karten, also hier fünf. Das Spiel kann so mit einer anderen Anzahl Bits auch für einen größeren oder kleineren Zahlenraum erstellt werden. In der folgenden Prezi zeige ich dir wie das Spiel funktioniert.
Das Spiel Magic Mind aus meinem Artikel Anzeige mobiler WebApps in WordPress basiert auf dem gleichen Prinzip. Hier erfolgt die Auswertung aber nicht durch einen Spielleiter, sondern automatisch durch ein Programm und anstatt der Zahlen werden Bilder verwendet. Das Spielalgorithmus ist identisch.
Automatisch im Browser abspielen
oder auf meinem YouTube-Kanal ansehen: MagicNumbers auf YouTube
MagicNumbers Karten zum drucken
Wenn du auf das Bild klickst kannst du dir eine PDF-Datei herunterladen, die Karten auf Karton drucken, ausscheiden und eine Menge Menschen sprachlos machen.
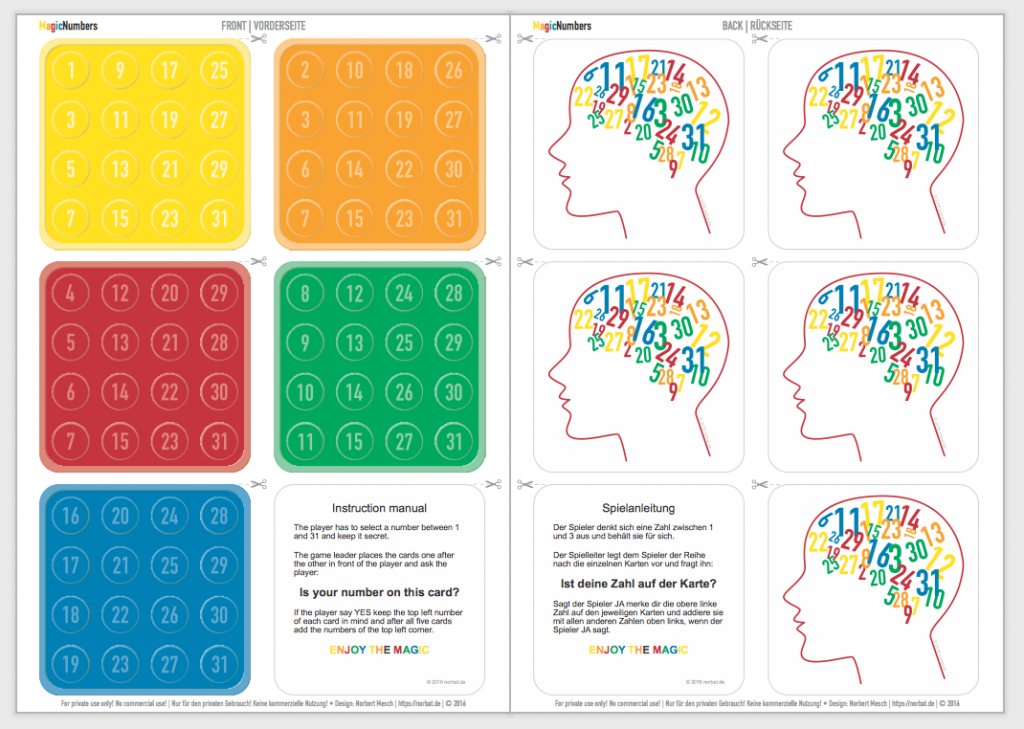
Die Druckvorlage ist für den privaten Gebrauch bestimmt. Eine kommerzielle Verwendung bedarf meiner schriftlichen Genehmigung.