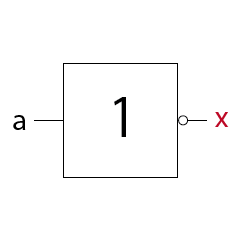
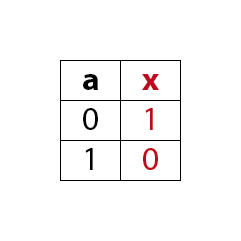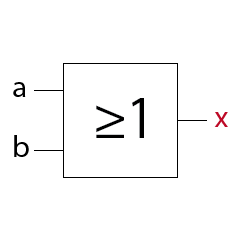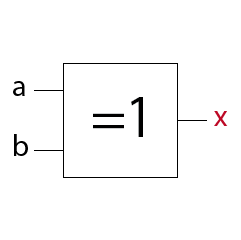Digitaltechnik – Verknüpfungsschaltungen

NICHT Schaltung (NOT)

Funktionsgleichung:

$x=\overline a$

Merksatz:

Liegt am Eingang a einer NICHT-Schaltung ein 0-Signal so liegt am Ausgang x ein 1-Signal.
Liegt am Eingang a einer NICHT-Schaltung ein 1-Signal so liegt am Ausgang x ein 0-Signal.
Ein NICHT-Gatter kehrt das Eingangssignal um.

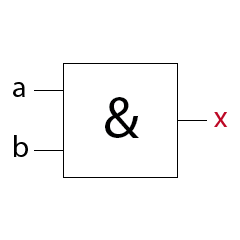
UND Schaltung (AND)

Funktionsgleichung:

$x=a\wedge b$

Merksatz:

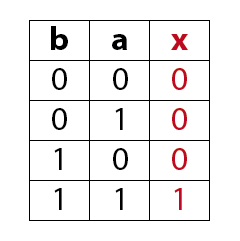
Liegt am Eingang a und am Eingang b einer UND-Schaltung ein 1-Signal so liegt am Ausgang x ein 1-Signal.
Ein UND-Gatter hat am Ausgang immer dann ein 1-Signal wenn alle Eingänge ein 1-Signal aufweisen.

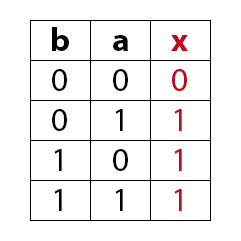
ODER Schaltung (OR)

Funktionsgleichung:

$x=a\vee b$

Merksatz:

Liegt am Eingang a oder am Eingang b einer ODER-Schaltung ein 1-Signal so liegt am Ausgang x ein 1-Signal.
Ein ODER-Gatter hat am Ausgang immer dann ein 1-Signal wenn mindestens ein Eingang ein 1-Signal aufweist.

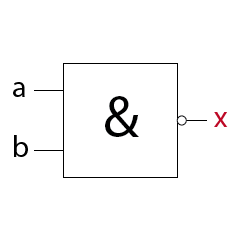
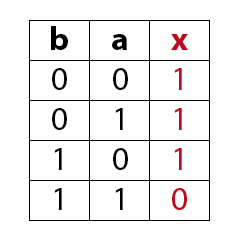
NOT-AND Schaltung (NAND)

Ein NAND-Gatter besteht aus deinem AND-Gatter mit negiertem Ausgang.

Funktionsgleichung:

$x=\overline { a\wedge b }$

Merksatz:

Ein NAND-Gatter hat am Ausgang immer dann ein 1-Signal wenn mindestens ein Eingang ein 0-Signal aufweist.

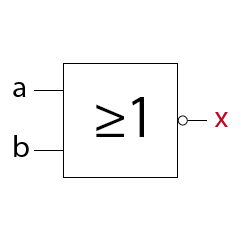
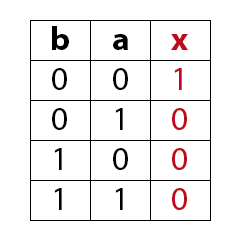
NOT–OR Schaltung (NOR)

Ein NOR-Gatter besteht aus einem OR-Gatter mit negiertem Ausgang.

Funktionsgleichung:

$x=\overline { a\vee b }$

Merksatz:

Ein NOR-Gatter hat am Ausgang immer dann ein 1-Signal wenn alle Eingänge ein 0-Signal aufweisen.

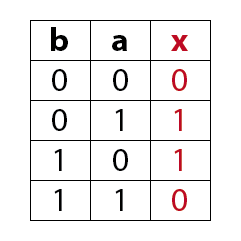
EXklusiv-OR Schaltung (XOR o. Antivalenzschaltung)

Funktionsgleichung:

$x=\left( a \wedge \overline b\right) \vee \left(\overline a\wedge b\right)$

Merksatz:

Ein XOR-Gatter mit zwei Eingängen hat am Ausgang immer dann ein 1-Signal wenn die Eingänge antivalente (entgegengesetzte) Signale aufweisen.

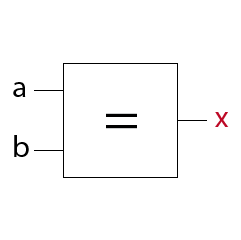
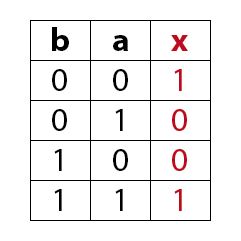
EXklusiv-NOT-OR Schaltung (XNOR o. Äquivalenzschaltung)

Funktionsgleichung:

$x=\left(\overline { a } \wedge \overline b\right) \vee \left(a\wedge b\right)$

Merksatz:

Ein XNOR-Gatter mit zwei Eingängen hat am Ausgang immer dann ein 1-Signal wenn die Eingänge äquivalente (gleiche) Eingangssignale aufweisen.

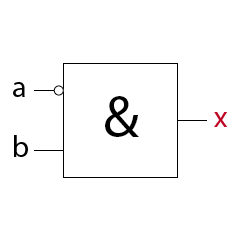
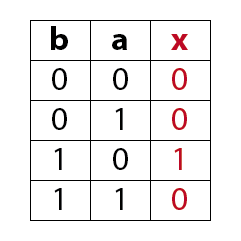
Inhibition (AND-Gatter mit Eingangsnegation o. Sperrgatter)

Im Beispiel handelt es sich um ein AND-Gatter mit einer Eingangsnegation am Eingang a.

Funktionsgleichung:

$x=\overline { a } \wedge b$

Merksatz:

Eine Inhibition hat am Ausgang immer dann ein 1-Signal wenn der nicht negierte Eingang ein 1-Signal und der negierte Eingang ein 0-Signal aufweisen.

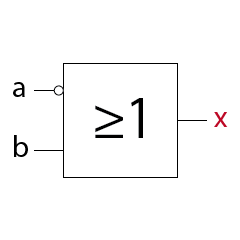
Implikation (OR-Gatter mit Eingangsnegation o. Subjunktion)

Im Beispiel handelt es sich um ein OR-Gatter mit einer Eingangsnegation am Eingang a.

Funktionsgleichung:

$x=\overline { a } \vee b$

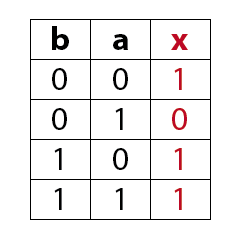
Merksatz:

Eine Implikation hat am Ausgang immer dann ein 1-Signal wenn der nicht negierte Eingang ein 1-Signal und der negierte Eingang ein 0-Signal aufweisen.