In diesem Beispiel zeige ich dir, wie du mit ein wenig Mathematik und JavaScript ein SVG Kreisdiagramm erstellen kannst.
Die Anzahl der Kreisstücke ist die Grundlage zur Ermittlung der Winkel für jedes einzelne Kreisstück. Bei vier Kreisstücken hat jedes Stück einen Winkel von 90° oder bei acht Kreisstücken einen Winkel von 45°. Der Winkel der Kreisstücke wird durch die Division eines Vollkreises (360°) durch die Anzahl der Teilstücke errechnet.
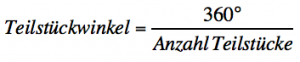
Hinweis: Die Kreisstücke in diesem Beispiel sind alle gleich groß. Wenn du das Beispiel durchgearbeitet hast, kannst du aber auch recht einfach Kreisdiagramme mit unterschiedlich großen Stücken erstellen.
Beispiel auf Codepen
See the Pen Calculated SVG pie chart by Norbert Mesch (@itsnorbat) on CodePen.
Mit Hilfe der Sinus- und Cosinus-Funktionen kannst du die Positionen der Koordinaten auf dem Kreisumfang errechnen. Das Kreisstück wird in SVG über ein path-Element konstruiert. Beachte bitte, dass JavaScript die Bogenmaße als Werte für die WInkelfunktionen benötigt.
Das folgende Beispiel zeigt dir das Rechenprinzip für ein Kreisstück von 30°, das bei 0° beginnt.
Die SVG-Datei ist auf 400 x 400 px angelegt. Der Mittelpunkt des Kreisdiagramms wird auf den Punkt mit der Koordinate 200,200 angelegt. An diesem Punkt beginnt auch das path-Element.
<?xml version="1.0" encoding="utf-8"?>
<svg version="1.1" id="piechart" xmlns="http://www.w3.org/2000/svg" x="0" y="0" width="400" height="400">
<desc>Pie chart constructed in SVG</desc>
<defs>
<pattern id="karo" x="0" y="0" width="20" height="20" patternUnits="userSpaceOnUse">
<rect x="0" y="0" width="20" height="20" fill="none" stroke="#000" stroke-width="0.5"></rect>
</pattern>
</defs>
<rect id="grid" x="0" y="0" width="400" height="400" fill="url(#karo)" stroke="#fff" stroke-width="0"/>
<g id="piechart" transform=""></g>
<g id="calcPie">
<path d="M200,200L200,380 A180,180 0 0,0 290,355.9z" style="fill: rgb(255, 0, 0);"></path>
<path d="M200,200L290,355.9 A180,180 0 0,0 355.9,290z" style="fill: rgb(255, 127, 0);"></path>
<path d="M200,200L355.9,290 A180,180 0 0,0 380,200z" style="fill: rgb(255, 255, 0);"></path>
<path d="M200,200L380,200 A180,180 0 0,0 355.9,110z" style="fill: rgb(128, 255, 0);"></path>
<path d="M200,200L355.9,110 A180,180 0 0,0 290,44.1z" style="fill: rgb(0, 255, 0);"></path>
<path d="M200,200L290,44.1 A180,180 0 0,0 200,20z" style="fill: rgb(0, 255, 128);"></path>
<path d="M200,200L200,20 A180,180 0 0,0 110,44.1z" style="fill: rgb(0, 255, 255);"></path>
<path d="M200,200L110,44.1 A180,180 0 0,0 44.1,110z" style="fill: rgb(0, 127, 255);"></path>
<path d="M200,200L44.1,110 A180,180 0 0,0 20,200z" style="fill: rgb(0, 0, 255);"></path>
<path d="M200,200L20,200 A180,180 0 0,0 44.1,290z" style="fill: rgb(127, 0, 255);"></path>
<path d="M200,200L44.1,290 A180,180 0 0,0 110,355.9z" style="fill: rgb(255, 0, 255);"></path>
<path d="M200,200L110,355.9 A180,180 0 0,0 200,380z" style="fill: rgb(255, 0, 128);"></path>
</g>
</svg>
Sehen wir uns jetzt das path-Element etwas genauer an. Koordinaten werden immer in der Reihenfolge x,y angegeben.
- Die erste Koordinate(200,200), die mit dem Buchstaben M (Moveto) eingeleitet wird, legt die Ursprungskoordinate des Pfades fest.
- Mit dem Kommando L (Lineto) und den anschließenden Koordinaten wird eine Linie zu genau diesem Punkt (380,200) gezogen.
- Das nächste Kommando A (elliptical Arc) ist etwas komplexer aufgebaut. Es beschreibt einen elliptischen Bogen. Die beiden ersten Koordinaten (180,180) beschreiben die Radien für die x- und y-Achse. Da es sich im hier gezeigten Fall um einen Kreis mit einem Radius von 180px handelt sind beide Radien gleich groß.
Der dritte Wert 0 beschreibt die Rotation der x-Achse um das aktuelle Koordinatensystem. Die 0 in diesem konkreten Fall bedeutet, dass die x-Achse nicht rotiert.
Der erste Wert des folgenden Wertepaares (0,1) beschreibt den kurzen Weg um die Ellipse (eine 1 beschreibt den langen Weg). Der zweite Wert beschreibt die Drehrichtung. Dabei bedeutet 1 = im Uhrzeigersinn und 0 = gegen den Uhrzeigersinn.
Die letzten Koordinaten (355.9,290) kennzeichnen den Endpunkt des elliptischen Bogens. - Das letzte Kommando z (closepath) schließt den Pfad auf dem kürzesten Weg von der letzten Koordinate zur ersten.
Ein bisschen Mathematik
Wie werden jetzt ausgehend von der Ursprungskoordinate im Kreismittelpunkt (200,200) die weiteren zwei Koordinatenpaare errechnet?
In diesem Beispiel gehen wir von einem Kreisstück von 30° aus. Das Kreisstück beginnt bei einem Winkel von 0° und hat einen Radius von 180.
Für das 2. Koordinatenpaar benötigen wird die x- und y-Werte bei einem Winkel von 0°.
Wir berechnen zunächst die Sinus- und Cosinus-Werte des Winkels von 0°
sin(0°) = 0, cos(0°) = 1
Diese Werte werden mit dem Radius unseres Kreises multipliziert und mit der jeweiligen Ursprungskoordinate addiert.
180 * 0 = 0, 180 * 1 = 180
x = 200 + 0 = 200, y = 200 + 180 = 380
(200,380)
weiter geht es mit den Koordinaten für den Winkel von 30°.
sin(30°) = 0.5, cos(30°) = 0.866
x = 200 + 180 * 0.5 = 290
y = 200 + 180 * 0.866 = 355.9
(290,355.9)
Jedes weitere Kreisstück wird lediglich mit einem anderen Anfangs- und Endwinkel berechnet. Im oben eingebetteten Pen kannst du dir dazu den Quelltext der For-Schleife ansehen.
@update 2015-10-19
Ich habe den Quelltext heute noch ein wenig geändert. Unter anderem habe ich die SMIL Animation aus dem Pen heraus genommen und durch CSS Keyframe Animationen ersetzt. Leider plant Google in zukünftigen Chrome Versionen die SMIL Funktionen von SVG nicht mehr zu unterstützen (weitere Details zu diesem Thema).
Außerdem habe ich noch eine Funktion zum Kopieren des SVG-Codes in den Pen implementiert. Damit kannst du dir ein Kreis- oder Regenschirmdiagramm einfach aus dem Pen kopieren und auf deiner Seite verwenden.
Hier siehst du ein paar Beispiele:

